How to Get Customer Networks?
Ein Artikel von Dr. Christian Michael Schneider, ehemaliger Mitarbeiter DYMATRIX
Network Theory and its Business Implication – Part 5
This post is about extracting a customer (social) network and evaluating the quality of the known part of the network. While the former task depends on the data sources of a company itself, the later one is (nearly) company independent. However, most companies have at least some kinds of customer-customer interactions. For example, travel agencies know who are traveling together, telecommunication companies have data about callers and callee, but also retailers can obtain interactions from friendship advertisement as well as family ties from personal customer data.
After collecting a certain amount of data, the question remains, if the data is sufficient to get significant information about the customers’ relationships. To illustrate this, the karate club network [1] from part 2 of this blog is used with different (random) fraction of known social interactions between the members ranging from 100% to 20% (top left to bottom right):
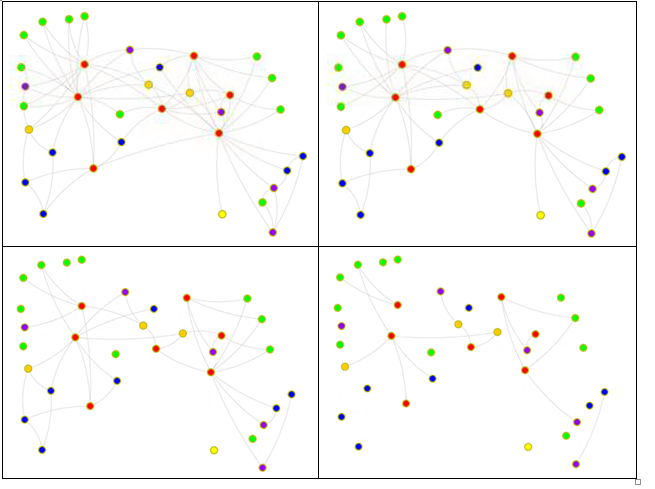
One can see that the main part of the social network remains connected, even if only half of the connection is known (bottom left). To generalize this behavior, the average degree (number of edges per node) is used. The network’s average degree is reduced from 4.5 over 3.3 and 2.2 to 1 (again from top left to bottom right) by randomly removing edges. From network theory for random networks one can classify the network into four groups [2]:
- < 1: There is no giant component (containing of nearly all customers, which are connected with each other through their friends), the size of the giant component growth logarithmically with the number of customers N and all cluster are trees (not shown in the above illustration).
- = 1: There is no giant component, the size of the giant component growth sublinear with the number of customers and the clusters may have loops (as shown bottom right; S = 10.5).
- > 1: A single giant component emerge with loops and all small clusters are trees (as shown top right and bottom left).
- > ln N: A single giant component emerge and no isolated customers exist (as shown top left; ln N = 3.5).
Though the theory is only for infinite large and random networks the results fit well with the real example network. Keeping this in mind, the initial question can be answered without knowing the full social network. To study the social network structure the number of interactions should be larger than half the number of customers. To get also local social information like friendships and communities, the number of social interactions should be larger than the logarithm of the number of customers.
Though the number of needed interactions remains high for random customer networks, observed social network are not random. Thus, I can close this chapter with good news, namely the required number of interactions for customer networks is about ≈ 2.
The final blog post is about using networks properties for modelling customer’s behavior.
Part 0. Network Theory and its Business Implication
Part 1. Identifying relevant business networks
Part 2. Is your customer or your customers’ friend more important for your business?
Part 3. How to identify product groups?
Part 4. How to keep your company happy and healthy?
Part 5. How to get customer (friendship) networks?
Part 6. Affinity modelling with network properties
[1] An information flow model for conflict and fission in small groups, W. W. Zachary, Journal of Anthropological Research 33 452-473, 1977
[2] On random graphs, P. Erdős and A. Rényi, I. Publicationes Mathematicae (Debrecen), 6 290-297, 1959



